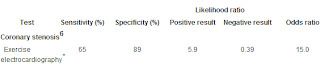Let It Bleed
Track 6
"Midnight Rambler" – 6:57
The Stones little "blues opera", as Keith called it. This is of course the studio version, over time less familiar than the live version from Get Yer Ya-Ya's Out! that is featured on every Stones compilation. Listening to it today, I was struck by how much smaller it sounded than the live version, how timid the band sounds. Not to say it is a bad track – it is probably the best example of the Stones playing straight blues in the studio. But it is yet another example of a song that was maybe recorded too quickly, and would have benefited from the experience of live performances to really get to know the strengths of the song.
Friday, July 4, 2008
Midnight Rambler
Tuesday, July 1, 2008
Sensitivity, Specificity, False Positives, and False Negatives (nonstones)
(As far from on-topic as possible – this post contains no Stones, no music, not even anything to do with popular culture. It is a post about statistics and medical tests. You have been warned.)
A couple of weeks ago a friend went to see a doctor to have a test done – she thought she might have a particular medical condition. The doctor reported that the test had come back positive. My friend told me this in tears – she was scared, petrified really, about having this condition. I tried to explain to her that a positive test did not necessarily mean what she thought it meant, and that she needed to know more before it was time to panic. I was unsuccessful in assuaging her fears, but I just heard today that I was right, that in this case a positive test result did not mean a positive result in real life.
I will attempt in this post to tell you what I tried (and failed) telling my friend about how to go about interpreting test results. There are dozens and dozens of posts like this one on the web. They are ubiquitous, I won't link to them. There is no reason to think I am explaining this any better than any one else could, but I have wanted to write something like this for years, just to have something I can point friends to when the situation arises again (and it will arise again). So here goes.
Take a look at the following numbers. They come from a table of numbers in an article in the BMJ – we'll look at only the first line. There is a specific test (electrocardiography) for the presence of a specific condition (coronary stenosis) – the numbers displayed show various statistical properties associated with this test (in terms of its accuracy in detecting the underlying condition). The numbers themselves aren’t important for this example – what they represent is. Few people understand them, but they are the most important part of any medical test results. I’ll explain each column. When you get any test result from your doctor, you should ask for these numbers, or ask for a lit reference so you can look them up yourself.
- Sensitivity: This number tells you the probability that, if you have the disease that you are being tested for, the test will find the disease. It does not apply if you don’t have the disease. Think of it in terms of a car alarm: if someone is breaking into your car in the parking lot, what is the probability that your car alarm will go off? Probably very high – I would guess the car alarm would go off maybe 95% of the time someone is trying to break into your car. The 95% number is Sensitivity. Medical tests typically have high sensitivity – in the tests listed, they average about 70% – it is 65% for the test in the above example. If you have coronary stenosis, and are tested for it by electrocardiography, the test will register a positive result 65% of the time. That means that if you have coronary stenosis, there is a 35% probability this test will fail to find it.
- Specificity: This is the probability that, if you DO NOT have the disease that you are being tested for, the test will register a negative result (that is, the correct result). This is a little complicated, because of the double negatives, but it is very important in terms of mental health. This number is rarely reported by doctors, and there have been studies that show they don’t really understand it well. YOU will understand it. You must understand it.
The tests listed have good specificity, and the one in my example above is very good – many tests do not discriminate this well. If a test has a specificity of 89% (like the one above), that means that if you don’t have coronary stenosis, there is still a 11% chance that it will tell you that you actually have the disease. Got that? You go into the test totally disease-free – there is a 1 in 9 chance that your doctor will tell you the test came up positive. ALL tests have this problem, and most tests have specificity rates much lower than 89%. If you ever get a positive result, DO NOT PANIC. Wait until the second test result, and then panic (second tests are usually much more accurate – and expensive, which is why they don't use them the first time).
Using the car alarm analogy, specificity is the probability that if no one is trying to steal your car, the car alarm will stay silent. But car alarms go off all the time, for no reason at all. Car alarms have poor specificity.
- Positive Likelihood, or Positive Predictive Value (PPV): This is the odds (or probability) that, if your test results come up positive, that you actually have the disease. The numbers below are reported as odds, which are terrible numbers for humans to deal will, but it is a simple calculation to convert them to probabilities. The test above has a positive likelihood of 5.9, meaning that if you take a test and the results come back positive, it is 5.9 times more likely that you actually have the disease than not. In terms of probability
Probability = Odds/(1+Odds)= 5.9/(1+5.9)= 86%
That means there is a 86% chance that your positive test result is correct, and a 14% chance that it is wrong.
There is a difference in the calculation of Positive Likelihood and Positive Predictive Value for some reason. To me, PPV is the more natural number: it is calculated by taking the number of people who actually had the disease AND tested positive (that is, the positive test result was correct) and dividing by the total number of people who tested positive (including those who didn't have the disease). In the scenario above, the 14% chance number is known as the false positive rate. In car alarm terms, the PPV is the probability that if your car alarm goes off that means someone is actually breaking into your car. As we know, car alarms have really low Positive Predictive Values, and high False Positive Rates. They go off all the time, and most of the time when they go off there is no one trying to break into them.
However, Positive Likelihood is a little different. I won't explain the difference here (it's complicated to explain), but will just say that it reports an analogous number to PPV, and is apparently less sensitive to the prevalence of the disease. The two numbers are similar (after you covert Positive Likelihood from a ratio into a probability), and you really want to know that False Positve Rate.
Note the difference between PPV (and Positive Likelihood) and Sensitivity. Sensitivity starts with the premise that someone is actually breaking into your car (i.e. you actually have the disease), and is telling you the probability that the alarm will go off (i.e. the test will return a positive result). PPV starts with the opposite premise, that your car alarm is already wailing away (i.e. you have a positive test result) and is telling you the probability that someone is actually breaking into your car (i.e. you actually have the disease).
- Negative Likelihood, or Negative Predictive Value (NPV): This is the odds (or probability) that, if your test results come up negative, that you actually have the disease regardless. The tests listed have a negative likelihood of .39, meaning that if you take a test and the results come back negative there is still a 28% chance that you actually have the disease (odds of .39 is equal to a probability of .39/(1 + .39) = 28%) . This is known as the false negative rate, and like specificity it is poorly understood because of the negatives.
(Again, note the difference in calcuation between Negative Likelihood and Negative Predictive Value, explained in the previous bullet. Both numbers are trying to tell you the same thing, even if they produce slightly different results.)
In the car alarm analogy, NPV is the probability that, if your car alarm is silent, there is in fact someone breaking into your car, and that if you get a negative test result, you really have the disease. Note the similarity to Specificity which gives you the probability that if nobody is breaking into your car, your car alarm stays silent.
Because we know better: overall accuracy throws away information, information that you will have in your hand that will give you better understanding of what these tests are doing. The information you will have is the test results: if you have a positive test result, you don’t care about overall accuracy, you care about the tests accuracy on positive results – the positive predictive value. (Or its False Positive Rate, which is 1 minus PPV.)
Or maybe you don’t yet have the tests results, but from some personal experience or strange feelings in your gut, you have some indication or suspicion that you have the disease. In this case, you want to know the test’s sensitivity – the ability of the test to find the disease if you actually have it.
Here is a rule of thumb: if the proportion of people who DO NOT have a disease is higher than a test’s sensitivity, the test will generate more FALSE positives that TRUE positives. That is, if a test has a sensitivity of 90% (which is a pretty high sensitivity rate), but the rate of infection in a population is 5% (i.e. 95% of people are not infected with the disease), it will generate positive results which are more often incorrect than correct – in this particular case, 81% of the positive test results will be wrong! Almost all medical tests fall within these conditions – i.e. the rate of people who don’t have the disease will be higher than a test’s sensitivity. Think of the car alarm: the overwhelming percentage of the time the car alarm is turned on, no one is trying to break into the car. But the car alarm itself is very sensitive. This almost guarantees that if the car alarm go off, it will be a false alarm. Medical tests are not as sensitive as car alarms, and perhaps many diseases are more likely to happen than car thefts, but the principle is the same.
The point is, if you ever get a positive result, wait until the second test result. Ask your doctor about false positive rates. Most of all, don't panic until you know more. Most positive test results are WRONG.
UPDATE Wed 2:23 PM: Changed some text to indicate the differences between Likelihood Ratios and Predictive Values.
Monday, June 30, 2008
Let It Bleed
Let It Bleed
Track 5
"Let It Bleed" – 5:34
I've been carrying around this theory for a while, that there are some words that are impossible to sing without sounding silly: "politician", "dingleberry", and, as "Let It Bleed" proves, "breasts" – Mick gives it about 4 syllables and a couple of extra s'es, and generally makes it sound like he's never encountered the word in his life.
You all recognise the "Honky Tonk Woman" drum pickup at the start of the track. Ian Stewart, "the sixth Stone", fills in on piano. (I'll let you in on a secret: I have never liked his piano playing. This is exactly the kind of song Nicky Hopkins could've taken over, but instead we get Stewart's rudimentary honky tonk piano playing.) But who is playing that wicked slide guitar? Various sources tend to be unanimous: it's Keith, blowing me away, once again, with the breadth of his talent.
Sunday, June 29, 2008
Live with Me
Let It Bleed
Track 4
"Live with Me" – 3:36
[Download here.]
Huh. I always thought "Bitch" came first. Go figure.
That's the instantly-identifiable Bobby Keys on sax – I didn't even have to look it up, his sound is unmistakable. This is his first recording with the Stones, but not his last – he will go on to play on virtually every album that follows, along with most of their tours.
That Charlie Watts four-on-the-floor really kicks ass. Mick really has his slur working. That Keith harmony in the verses is a neat touch. But overall, this is another one of those songs I've always loved but couldn't really explain why.